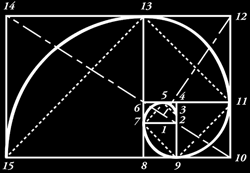
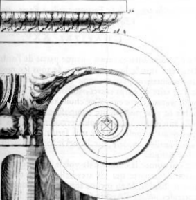
We look to forms in nature as strategies for design. The Golden Mean, 1:1.618034, represented by the Greek letter phi, is a naturally occurring number that repeatedly occurs in various relationships. Like pi, it is an irrational number. Unlike pi, it clearly and regularly appears in the growth patterns of many living things, like the spiral formed by a seashell or the curve of a fern. It is in fact the only growth pattern that, if continued, is not doomed to failure. It was derived by the ancient Greeks and used in the design of buildings and monuments.
Contact Us"Beauty is truth, truth beauty," - that is all Ye need know on earth
John Keats
They discovered they could create a feeling of natural order, as well as structural integrity, in their works. Artists since have used it for the same reason, to create a feeling of natural order in their works. In the l930's, Pratt Institute did a study on various rectangular proportions laid out as vertical frames, and asked several hundred art students to comment on which seemed the most pleasing. The Golden Ratio was favored by a very large margin, which seemed to point to the actual dimensions as generating a pleasing response by their size.

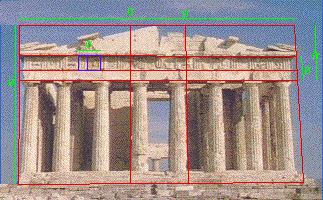
Plato said that a line so divided into two unequal segments so that the smaller bore the same relationship to the larger as the larger to the whole line, would represent a special kind of proportional relationship with important properties. Using the line segments above, AB is to BC as BC is to AC. Euclid discussed this relationship in his book on proportion in geometric terms, naturally stopping short of identifying exact numbers, which would have been inconceivable with the primitive Greek numerical system. That this was a commonly understood and accepted ratio can be inferred from its extensive use in the work of the 5th century architect Iktinos, who designed the Parthenon with the Golden ratio throughout.
Leonard of Pisa (1170-1250), better known as Fibonacci, introduced the Fibonacci Series, a sequence of numbers;
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1,597…
in which any number is the sum of the two preceding members.
0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, 5 + 8 = 13, etc.
The Fibonacci Series and the Golden Mean are intimately connected. The Fibonacci Series numbers increase at a rate equal to (actually, oscillating round) the Golden mean. (The larger the numbers, the closer to the Golden Mean.) A rectangle whose sides are related by phi (such as 13 x 8) is said to be a Golden Rectangle. Proportion is the relationship of the size of two things. Arithmetic proportion exists when a quantity is changed by adding some amount. Geometric proportion exists when a quantity is changed by multiplying by some amount. Phi possesses both qualities, and as such, is considered perfect proportion, also referred to as the Divine Proportion. From the Fibonacci Series and the Golden Rectangle we realize that: phi + 1 = phi x phi. From this relationship, we can calculate the value of phi. Thus we see that the Golden Mean proportion is both arithmetic and geometric. In pure mathematics, an increase in size can be any imaginable number, even one like e or p. But in the world of nature, things always grow by adding some unit, even if the unit is as small as a molecule. So it's not surprising that phi turns out to be an ideal rate of growth for things which grow by adding some quantity.
Some examples: The Nautilus shell (Nautilus pompilius) grows larger on each spiral by phi. The sunflower has 55 clockwise spirals overlaid on either 34 or 89) counterclockwise spirals, a phi proportion.
3 petals: lily, iris Often lilies have 6 petals formed from two sets of 3.
5 petals: buttercup, wild rose, larkspur, columbine.
8 petals: delphiniums
13 petals: ragwort, corn marigold, cineraria,
21 petals: aster, black-eyed susan, chicory
34 petals: plantain, pyrethrum
With objects occurring in nature, there is diversity due to age, diet, weather, and a host of other variables. With natural Phi relationships, we see the illustrated concept even though it may not be strictly mathematical.

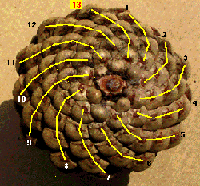
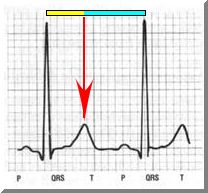
Pine cones show the Fibonacci Spirals clearly. Here is a picture of an ordinary pinecone seen from its base where the stalk connects it to the tree. A normal human heart beats in a phi rhythm, with the T point of a normal electrocardiogram (ECG or EKG) falling at the phi point of the heart's rhythmic cycle. Prominent parts of the ECG are the P wave, a deflection caused by the current originating in the atrium; the QRS complex, showing the passage of the electrical activity into the ventricles; and the T wave, as the ventricles reset themselves.
In Exodus 25:10, God commands Moses to build the Ark of the Covenant, in which to hold His Covenant with the Israelites, the Ten Commandments, saying, "Have them make a chest of acacia wood, two and a half cubits long, a cubit and a half wide, and a cubit and a half high." The ratio of 2.5 to 1.5 is 1.667..., which is as close to phi (1.618...) as you can come with such simple numbers and is certainly not visibly different to the eye. The Ark of the Covenant is thus constructed using the Golden Section. This ratio is also the same as 5 to 3, numbers from the Fibonacci series. In Genesis 6:15, God commands Noah to build an ark saying, "And this is the fashion which thou shalt make it of: The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits." Thus the end of the ark, at 50 by 30 cubits, is also in the ratio of 5 to 3, or 1.667..., again a close approximation of phi not visibly different to the naked eye.
Even music has a foundation in the series, as: 13 notes separate each octave of 8 notes in a scale, of which the 5th and 3rd notes create the basic foundation of all chords, and are based on whole tone which is 2 steps from the root tone, that is the 1st note of the scale. Note too how the piano keyboard scale of 13 keys has 8 white keys and 5 black keys, split into groups of 3 and 2.